Your browser doesn't support the features required by impress.js, so you are presented with a simplified version of this presentation.

For the best experience please use the latest Chrome, Safari or Firefox browser.

P2I7 - Modélisation Numérique pour l'ingénieur

Projet 20 - Modélisation de la vibration d'une corde de violon
intro
Moises Torres insa

Le violon



violon

Problématique

Construire un modèle suffisamment simple pour être approché numériquement pour reproduire l'essentiel du son caractéristique du violon.

Le processus de modélisation numérique

processu modelisation numerique

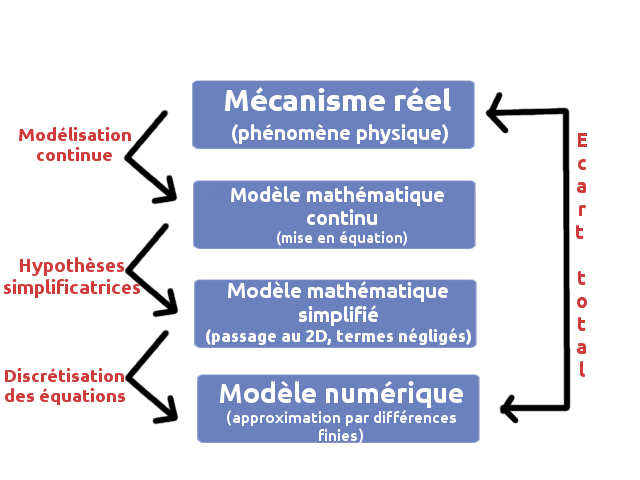
Simplification


Étape 1

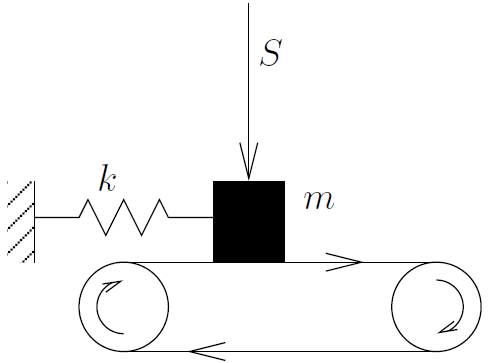etape1 Etudier le mouvement d'une masselotte attachée par des ressorts à un support fixe et sur laquelle l'archet vient frotter.

Étape 2

Remplacer la corde par une série de masselottes reliées par des ressorts et en ne faisant frotter qu'une masselotte.

etape2

Premier modèle


Modèle continu

En considérant la loi de frottement de Coulomb on applique le Principe Fondamental de la Dynamique à la masselotte.

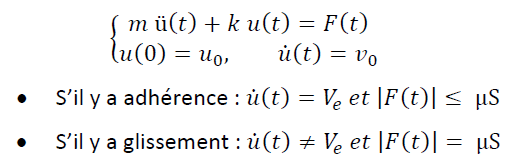
mise en equation

Ve: Vitesse de glissement de la mèche de l'archet.
S: Force d'appui de la mèche de l'archet.
k: raideur de l'archet.
m: masse de la masselotte.
mu: Coefficient de frottement (Une fonction de la vitesse de glissement).

* Glissement et Adhérence, les deux phases du phénomène de "Stick and Slip".

Deuxième modèle


La masselotte en contact avec l'archet est attachée à des masselottes.


Hypothèses simplificatrices

- Force longitudinale négligée car très faible.
- Fréquence de la corde correspond à la fréquence d'oscillation de la masselotte.

etape2

Problème mathématique en forme matriciel

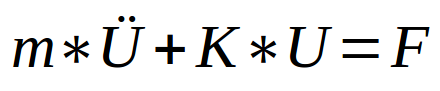
probleme matriciel
Passage en modèle numérique

Discrétisation des équations

Méthodes numériques:

- Schéma implicite d'Euler (plus de stabilité).
- Méthode des différences finies.

Utilisation de Matlab (logiciel privateur) et GNU Octave (logiciel libre) pour la programmation.

Algorithme de calcul

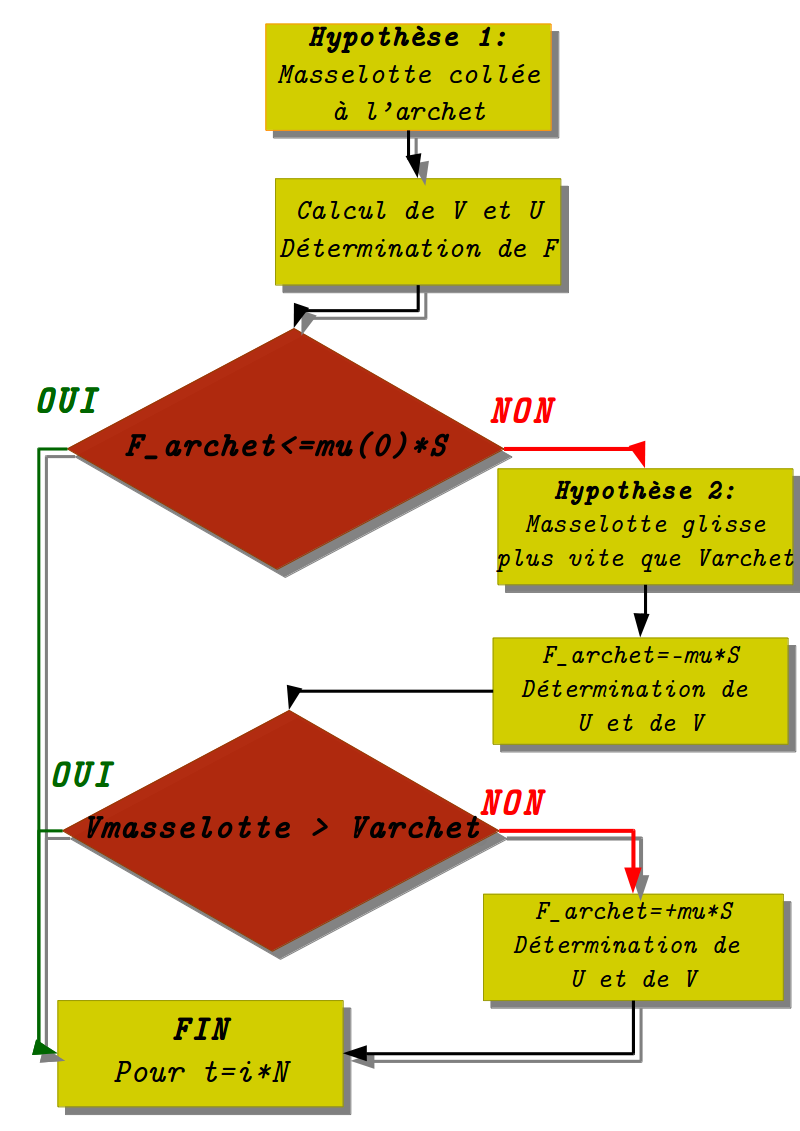
algorithme

Résultats


Graphiques


Paramètres: L=1m, Nbr. Masselottes=70, position archet=35
m=0.5kg, S=0.3N, k=0.9 N/m, Ve=0.5 m/s.

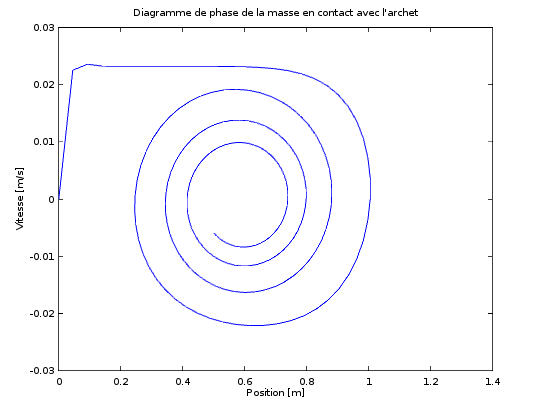
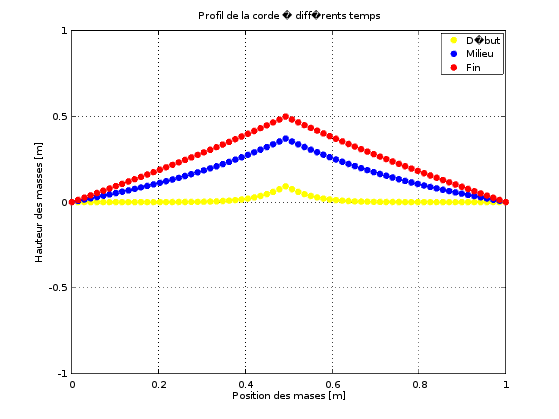
phase corde

Représentation de la corde à trois moments.
Diagramme de phase.

misc


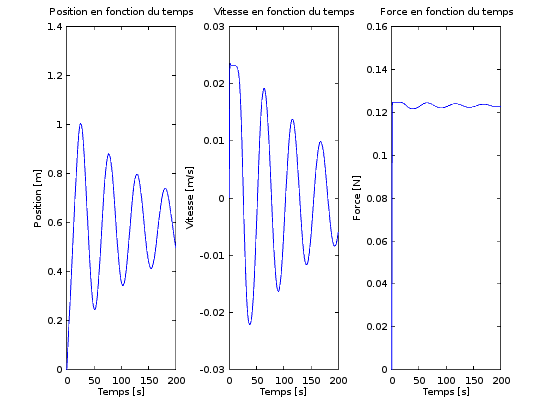
En haut, position, vitesse et force en fonction du temps.
On remarque la convergence de la solution.

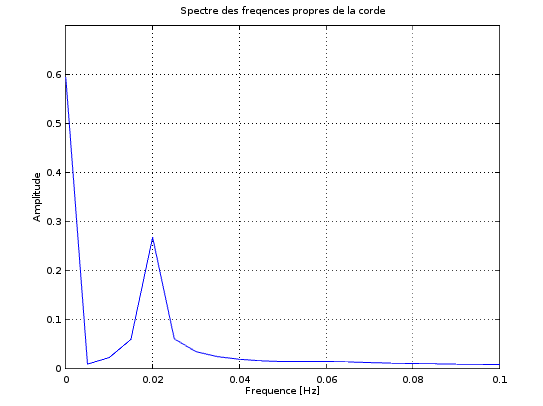
A gauche, le spectre de fréquences.
La fréquence obtenue est très faible.

spectre

Animation


Conclusion



Malheureusement nos modèles sont loin d'être parfaits.
Cet écart est dû principalement à des hypothèses simplificatrices et des méthodes numériques utilisées:

  • Action perpendiculaire de l'archet sur la corde (l'angle peut influencer).
  • Prise en compte des forces transversales (Les forces longitudinales pourrait influencer à long terme).
  • La fréquence de la corde correspond à la fréquence de l'oscillation masselotte-archet. (Les oscillations de chaque masselotte jouent un rôle dans la fréquence de la corde).
  • Schéma implicite. (D'autres schémas pourrait nous donner de meilleurs résultats).

    • Use a spacebar or arrow keys to navigate